MATEMÁTICAS V SEMESTRE!!!

TEMA 1:

 *RELEVANCIA DE LA PROFESIÓN DOCENTE EN LA ESCUELA DEL NUEVO MILENIO. 

INTRODUCCIÓN*

•La competencia de las personas en el mundo actual  se mide en términos de la respuesta que tienen ante los problemas que enfrentan.

•Los maestros fortalecen las capacidades intelectuales de los estudiantes potenciando aprendizajes significativos.

•Las competencias a enseñar es darles las herramientas para que sigan aprendiendo a lo largo se su vida .

•La sociedad exige de los docentes conocimientos que van mas allá de su formación inicial y de la propia experiencia.

•Requiere de nuevas capacidades para el pensamiento, planificar, desarrollar y evaluar la clase formativamente.

•Atender a el aprendizaje previo y desarrollar ambientes aptos para este.

•Diseñar estrategias para estimular el esfuerzo de los alumnos, promover su capacidad para aprender por si mismos.

•Acercarse a las tecnologías de la comunicación.

•Formar hábitos y transmitir disposiciones éticas.

La Reforma Integral de la Educación Básica

Es una puerta que invita a la:

•profesionalización continua

•oportunidades de crecimiento personal

•renovación de saberes

•evaluación de la intervención pedagógica

•Incorporación de nuevos materiales

•Competencias para la vida

Los paradigmas educativos que deben tener los profesores del siglo XXI

•*aprender a aprender. _ sentar las bases en la formación para aprender toda la vida.

•*aprender a hacer._ la acción de movilización de los conocimientos.

•*aprender a ser._ seres meramente racionales.

•*aprender a convivir._ aprender a ser seres humanos y personas .

*Prácticas sin cavidad en el aula:

•Disciplina que limita derechos.

•Descontextualización

•Homogeneización  y normalización

•Autoritarismo

*RELEVANCIA DE LA PROFESIÓN DOCENTE*

•Un profesor trabaja para la eternidad; nadie puede predecir en donde acabará su influencia.

•la practica docente se entiende como un proceso formativo que le compete a cada maestro pero también a la sociedad.

•En cada nuevo ciclo escolar los docentes en servicio fortalecen sus competencias  para lograr el desarrollo pleno e integral del educando.

CONCURSO DE ALTARES

MATEMÁTICAS V SEMESTRE*

El teorema de Pitágoras

En primer lugar deberíamos recordar un par de ideas:
 
• Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
• En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.
Teorema de Pitágoras.- En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.


Demostración:

Si tenemos un triángulo rectángulo como el del dibujo del enunciado del teorema podemos construir un cuadrado que tenga de lado justo lo que mide el cateto b, más lo que mide el cateto c, es decir b+c, como en la figura de la derecha.
El área de este cuadrado será (b+c)².
Si ahora trazamos las hipotenusas de los triángulos rectángulos que salen tendremos la figura de la izquierda. El área del cuadrado, que es la misma de antes, se puede poner ahora como la suma de las áreas de los cuatro triángulos rectángulos azules (base por altura partido por 2):

más el área del cuadrado amarillo . Es decir, el área del cuadrado grande también es el área del cuadrado pequeño más 4 veces el área del triángulo:
Podemos igualar las dos formas de calcular el área del cuadrado grande y tenemos:si ahora desarrollamos el binomio , nos queda:que después de simplificar resulta lo que estábamos buscando:

CONGRUENCIA DE LOS TRIÁNGULOS*

La congruencia de triángulos se basa en el estudio de la igualdad entre triángulos, es decir, gracias a esto podemos saber si esos dos triángulos o más son congruentes (iguales) entre sí. Dicho de modo sencillo, nos permite comparar varios triángulos y saber si son iguales (si tienen los mismos ángulos en sus vértices y si sus lados miden lo mismo).

Entonces, sabemos que si dos triángulos tienen tres ángulos y tres lados iguales entre si, son iguales ( o congruentes), ahora bien, no es necesario en todos los casos verificar uno a uno todos esos elementos. Hay veces que con mirar tres pares de elementos nos llega, para ello vamos a utilizar los llamados criterios de congruencia, viendo cada una de las posibilidades por separado:

1º LLL (LADO, LADO, LADO)

Considerando dos triángulos de lados a, b y c y a´, b´ y c´, se dice que son congruentes, si sus lados son iguales entre sí, es decir:

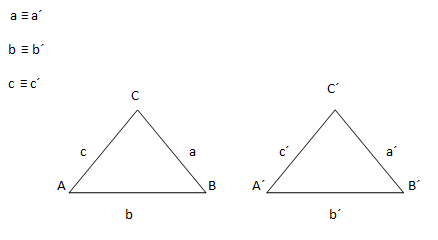
**Pista**: Las letras en mayúscula denotan los vértices, mientras que las minúsculas se refieren a los lados, mas adelante usaremos letras griegas (beta, gamma) para referirnos a los ángulos, es solo nomenclatura establecida, es decir, es así porque se pusieron de acuerdo entre todos.

2º LAL (LADO, ÁNGULO, LADO)

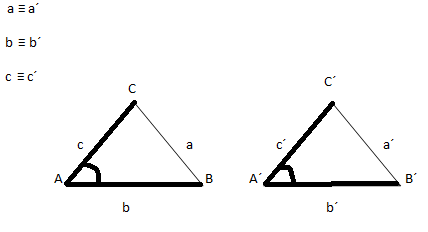
Considerando los mismos triángulos de lados a, b y c y a´, b´ y c´ respectivamente, se dice que son congruentes si tienen dos lados iguales y el ángulo que se forma con la unión de estos (en el vértice).

En este caso hemos subrayado en negrita los lados congruentes que forman los ángulos α y α´, también congruentes entre ellos, es decir, que tienen la misma amplitud.

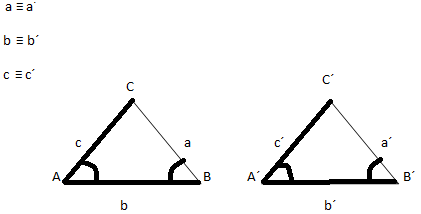
3º ALA (ANGULO, LADO, ANGULO)

Teniendo un lado igual (que mida lo mismo, es decir, que sea congruente), y con los ángulos que se forman en los extremos de dicho lado también congruentes. A estos ángulos se les denomina adyacentes al lado y los denominaremos α y β y α´ y β´ para los del otro triángulo.

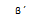
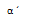
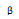
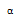
4º LLA (LADO, LADO ANGULO)

Con dos lados iguales (congruentes) y los ángulos opuestos al mayor de los lados también son congruentes.

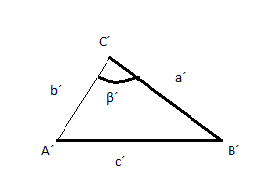
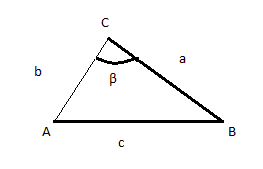
Considerando beta y beta prima ángulo iguales y lo mismo para ay b con sus homónimos a´ y b´.

BY*GIOVANNITHA*

Rectas y puntos notables en un triángulo

En los triángulos hay una serie de rectas y puntos importantes. Las rectas son la mediana, la mediatriz, la altura y la bisectriz. Los puntos donde se cortan son el baricentro, el circuncentro, el ortocentro y el incentro, respectivamente.

Medianas

 

Saber másEl centro de gravedad

Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centro de gravedad del triángulo.

Las medianas de un triángulo son las rectas que se obtienen al unir cada uno de los vértices del triángulo con el punto medio del lado opuesto a él.

Las tres medianas de un triángulo se cortan en un punto que se llama  baricentro.

Mediatrices

 

Saber másCircunferencia circunscrita

Todos los puntos de la mediatriz equidistan de los extremos del segmento. El circuncentro se encuentra a la misma distancia de los tres vértices.

Las mediatrices de un triángulo son las rectas perpendiculares a sus lados que pasan por el punto medio.

Se cortan en un punto que está a la misma distancia de los tres vértices del triángulo. Ese punto se denomina circuncentro.

Con centro en el circuncentro, y radio la distancia del circuncentro a un vértice, dibujamos una circunferencia que pasa por los tres vértices; es la circunferencia circunscrita al triángulo.

Alturas

Las alturas de un triángulo son las rectas perpendiculares que van desde un vértice al lado opuesto o a su prolongación.

Las tres alturas de un triángulo se cortan en un punto que se llama ortocentro.

Bisectrices

Las bisectrices de un triángulo son las rectas que dividen a sus ángulos en dos partes iguales.

Las bisectrices de un triángulo se cortan en un punto llamado incentro.

Con centro en el incentro, y radio la distancia de este punto a cualquiera de los lados del triángulo, se puede trazar una circunferencia tangente a los tres lados del triángulo: es la circunferencia inscrita.

TRIÁNGULOS*

Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.

Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 lados y 3 vértices.

CLASIFICACIÓN DE LOS TRIÁNGULOS*

Los triángulos se pueden clasificar por la relación entre las longitudes de sus lados o por la amplitud de sus ángulos.

Por las longitudes de sus lados

Por las longitudes de sus lados, todo triángulo se clasifica:

• como triángulo equilátero, y susu 3 lados no tienen la misma longitud (los tres ángulos internos miden 60 grados ó  radianes.)

• como triángulo isósceles  si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida. (Tales de Mileto, filósofo griego, demostró que un triángulo isósceles tiene dos ángulos iguales, estableciendo así una relación entre longitudes y ángulos; a lados iguales, ángulos iguales¹ ), y
• como triángulo escaleno  si todos sus lados tienen longitudes diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma medida).

                                   Equilátero           Isósceles                      Escaleno

Por la amplitud de sus ángulos*

Por la amplitud de sus ángulos, los triángulos se clasifican en:

(Clasificación por amplitud de sus ángulos) Triángulos Rectángulos Oblicuángulos Obtusángulos Acutángulos

• Triángulo rectángulo: si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto seles denomina catetos y al otro lado hipotenusa.
• Triángulo oblicuángulo: cuando ninguno de sus ángulos interiores son rectos (90°). Por ello, los triángulos obtusángulos y acutángulos son oblicuángulos.Triángulo obtusángulo: si uno de sus ángulos interiores es obtuso (mayor de 90°); los otros dos son agudos (menores de 90°).
• Triángulo acutángulo: cuando sus tres ángulos interiores son menores de 90°. El triángulo equilátero es un caso particular de triángulo acutángulo.

Rectángulo	Obtusángulo	Acutángulo
	Oblicuángulos Clasificación según los lados y los ángulos Los triángulos acutángulos pueden ser: Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto. Este triángulo es simétrico respecto de su altura. Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene eje de simetría. Triángulo acutángulo equilátero: sus tres lados y sus tres ángulos son iguales; las tres alturas son ejes de simetría (dividen al triángulo en dos triángulos iguales). Los triángulos rectángulos pueden ser: Triángulo rectángulo isósceles: con un ángulo recto y dos agudos iguales (de 45° cada uno), dos lados son iguales y el otro diferente: los lados iguales son los catetos y el diferente es la hipotenusa. Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo recto. Triángulo rectángulo escaleno: tiene un ángulo recto, y todos sus lados y ángulos son diferentes. Los triángulos obtusángulos pueden ser: Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que forman el ángulo obtuso; el otro lado es mayor que éstos dos. Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.