CONGRUENCIA DE LOS TRIÁNGULOS*
La congruencia de triángulos se basa en el estudio de la igualdad entre triángulos, es decir, gracias a esto podemos saber si esos dos triángulos o más son congruentes (iguales) entre sí. Dicho de modo sencillo, nos permite comparar varios triángulos y saber si son iguales (si tienen los mismos ángulos en sus vértices y si sus lados miden lo mismo).
Entonces, sabemos que si dos triángulos tienen tres ángulos y tres lados iguales entre si, son iguales ( o congruentes), ahora bien, no es necesario en todos los casos verificar uno a uno todos esos elementos. Hay veces que con mirar tres pares de elementos nos llega, para ello vamos a utilizar los llamados criterios de congruencia, viendo cada una de las posibilidades por separado:
1º LLL (LADO, LADO, LADO)
Considerando dos triángulos de lados a, b y c y a´, b´ y c´, se dice que son congruentes, si sus lados son iguales entre sí, es decir:
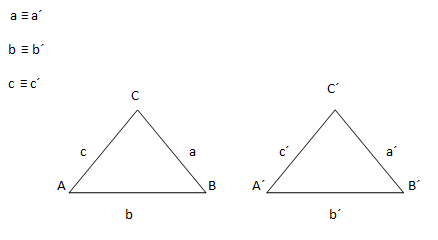
**Pista**: Las letras en mayúscula denotan los vértices, mientras que las minúsculas se refieren a los lados, mas adelante usaremos letras griegas (beta, gamma) para referirnos a los ángulos, es solo nomenclatura establecida, es decir, es así porque se pusieron de acuerdo entre todos.
2º LAL (LADO, ÁNGULO, LADO)
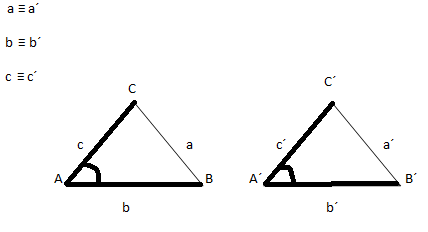
Considerando los mismos triángulos de lados a, b y c y a´, b´ y c´ respectivamente, se dice que son congruentes si tienen dos lados iguales y el ángulo que se forma con la unión de estos (en el vértice).
En este caso hemos subrayado en negrita los lados congruentes que forman los ángulos α y α´, también congruentes entre ellos, es decir, que tienen la misma amplitud.
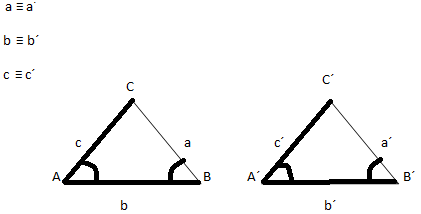
3º ALA (ANGULO, LADO, ANGULO)
Teniendo un lado igual (que mida lo mismo, es decir, que sea congruente), y con los ángulos que se forman en los extremos de dicho lado también congruentes. A estos ángulos se les denomina adyacentes al lado y los denominaremos α y β y α´ y β´ para los del otro triángulo.
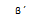
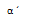
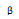
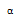
4º LLA (LADO, LADO ANGULO)
Con dos lados iguales (congruentes) y los ángulos opuestos al mayor de los lados también son congruentes.
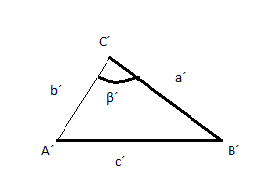
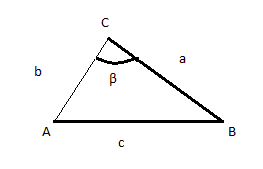
Considerando beta y beta prima ángulo iguales y lo mismo para ay b con sus homónimos a´ y b´.
BY*GIOVANNITHA*
No hay comentarios:
Publicar un comentario